Formulas for Euler’s Totient Function
I wish to share some intriguing formulas that I have recently discovered for Euler’s totient function, denoted as ![]() .
.
Formulas
I claim that these formulas are proved, though I omit the details for now. The formulas and their proofs will soon be added to a recent paper of mine: Elementary Formulas for Greatest Common Divisors and Semiprime Factors.
For all ![]() , we have:
, we have:
(1) 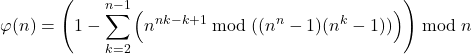
(2) 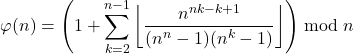
(3) 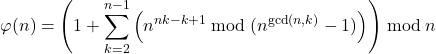
Conjectures
I leave the following as conjectures.
Conjecture 1. Let ![]() such that
such that ![]() is not congruent to
is not congruent to ![]() mod
mod ![]() . Then
. Then
(4) 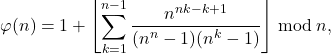
(5) 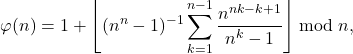
and
(6) 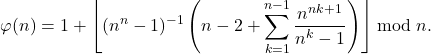
Otherwise
(7) 
Conjecture 2. Let ![]() such that
such that ![]() is not a phi-practical number whose divisors have distinct values of the Euler totient function (See A359417). Then
is not a phi-practical number whose divisors have distinct values of the Euler totient function (See A359417). Then
(8) ![Rendered by QuickLaTeX.com \begin{align*} \varphi(n) = \left[ \sum_{k=1}^{n-1} \frac{n^{nk-k+1}}{(n^n-1)(n^k-1)} \right] \bmod n \end{align*}](https://www.josephshunia.com/wp-content/ql-cache/quicklatex.com-d59601abb9934711f236fcb3e43dc2c5_l3.png)
and
(9) ![Rendered by QuickLaTeX.com \begin{align*} \varphi(n) = \left[ (n^n-1)^{-1} \sum_{k=1}^{n-1} \frac{n^{nk-k+1}}{n^k-1} \right] \bmod n , \end{align*}](https://www.josephshunia.com/wp-content/ql-cache/quicklatex.com-85e44ddca63b1a5a1fd898d9f3a7eac7_l3.png)
where the term inside of the brackets is rounded to the nearest integer.
Conjecture 3. Let ![]() . Then
. Then

Conjecture 4. Let ![]() . Then
. Then
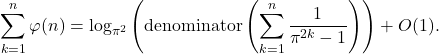
Conjecture 5.
Let ![]() . Then
. Then

Conjecture 6.
![]()
where ![]() returns
returns ![]() if
if ![]() is a product of exactly two distinct primes, and
is a product of exactly two distinct primes, and ![]() otherwise.
otherwise.
Comments are closed.